Dans tous les livres scolaires, on trouvait alors des exercices de bassins qui se remplissent, de fontaines qui coulent, de champs à clôturer ou de récoltes à vendre. Ce type de problème correspond alors à une France encore très rurale dans laquelle les paysans constituent une part importante de la population active. Aussi, le certificat d’études a-t-il pour fonction d’assurer à la majorité des jeunes qui le passent de solides bases de calcul ainsi qu’une bonne connaissance des unités de mesure dont ils auront un usage quotidien au village comme à la ferme.

De tous les exercices de calcul proposés, ceux qui concernent l’eau qui coule des fontaines, remplit les bassins, sont les plus courants. Ils sont en prise avec la vie des villages dans lesquels plus de 80% des logements ne possèdent pas l’eau courante, nécessitant de se rendre quotidiennement à la fontaine publique. Installée à l’entrée de la rue de la Poste, celle d’Albens a été réalisée en 1836 sous le règne du roi de Piémont-Sardaigne Charles Albert. Dans les années 50, son modeste débit peut faire écho au problème suivant : « Une fontaine donne 25 litres d’eau en 14 minutes. Une autre donne 41 litres en 21 minutes. Quelle fontaine débite le plus d’eau dans le même temps ? Au bout de combien de temps, la fontaine qui coule le plus vite aura-t-elle donné 100 litres de plus que l’autre ? ». Dans le village de Braille c’est le magnifique bassin qui peut entrer en résonnance avec cet énoncé : « Un bassin mesure 1m75 de large, 4m50 de long, et 1m80 de profondeur. On le remplit grâce à un robinet qui débite 82 litres par minute. Combien de temps faudra-t-il pour remplir ce bassin ? ».

Pour réussir tous ces problèmes et bien d’autres, il faut être capable de jongler avec les litres, hectolitres, ares et hectares, mètres et kilomètres, bien savoir que soixante secondes font une minute et soixante d’entre elles s’écoulent durant une heure. Le protège-cahier, avec ses illustrations, est là pour nous aider à mémoriser toutes ces unités. On y trouve par exemple la représentation des diverses mesures pour les liquides, en étain pour le vin, en fer blanc pour le lait ou pour l’huile.
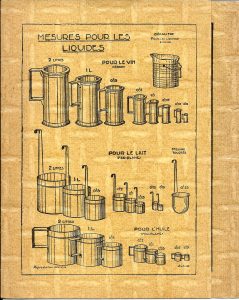
Leurs formes sont alors familières aux enfants des régions céréalières comme de celles tournées vers la viticulture ou l’élevage laitier. De cette façon, on ne doit pas être surpris d’avoir à résoudre pour un éleveur le problème suivant : « Un cultivateur possède 5 vaches qui lui procurent en moyenne chacune 8 litres de lait par jour. De 2 litres de lait, on retire 20 centilitres de crème et 1 litre de crème donne 250 grammes de beurre. Si le beurre vaut 56 francs le kilo, calculez quelle somme rapporte au cultivateur en une semaine, ses 5 vaches ».
La rédaction de ces exercices demandait aux jeunes élèves d’effectuer une lecture très attentive. Avant de se lancer dans les calculs, il fallait bien avoir compris l’histoire racontée, bien identifier les différentes unités que l’on allait utiliser. Ensuite, il était temps de se lancer dans la résolution du problème en prenant bien soin d’écrire de façon lisible toutes les opérations avant, au final, de rédiger la réponse. Un exercice qui pouvait en perdre plus d’un.
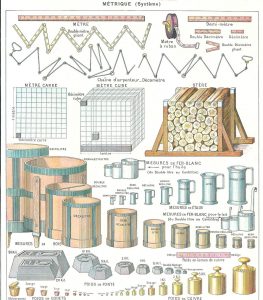
Les histoires qui habillaient ces exercices se rapportaient le plus souvent au monde agricole. Tantôt il fallait calculer un volume de bois, d’autre fois clôturer un champ dont on devait calculer le périmètre, prévoir le nombre de piquets nécessaire, sans oublier l’installation d’une porte. Mais le plus souvent il était question des récoltes : « Un cultivateur a récolté 126 hectolitres de blé dont il a vendu la moitié au prix de 750 francs le quintal (100 kilos). Combien cette vente lui a-t-elle rapporté, si l’hectolitre de blé pèse 81kilogrammes ? ». Après avoir jonglé avec les hectolitres et les quintaux, un autre exercice vous plongeait dans des calculs de rendement et la valse des hectares, kilos, ares et quintaux. Dans celui-ci, il est question de récolte de pommes de terre : « Un cultivateur a planté en pommes de terre un champ de 2 hectares et demi. Le rendement moyen est de 180 kg l’are. Évaluer en quintaux le poids de la récolte. Cette récolte est vendue en trois fois : un tiers à l’arrachage à 12,50 F le quintal ; la moitié du reste au début de l’hiver à 150 F la tonne. Le reste des pommes de terre n’est vendu qu’au mois de mars à 17,40 F le quintal, mais le cultivateur constate un déchet de 10%. Quelle somme retirera-t-il de sa récolte ».
Tous les exercices ne tournaient pas autour des réalités agricoles. Avec les sujets portant sur la circulation des trains, le calcul nous faisait entrer dans le monde plus moderne des transports, la voie ferrée étant alors le moyen de transport le plus populaire.

C’est le temps où la SNCF se lance avec succès dans la modernité avec l’électrification de la traction et du réseau. Ces réussites sont célébrées par la presse enfantine : « Avec les CC 7107 et BB 9004 qui ont roulé à 330 km/h, la France détient le record du monde sur rail. Ce record absolu a permis d’améliorer la vitesse commerciale sur les lignes électrifiées, si bien que nous possédons les trains les plus rapides du monde sur des distances de plus de 500 km, notamment avec le « Mistral », qui relie Paris à Marseille ».
Dans nos livres de calcul, les trains ne roulaient pas aussi vite, jugez-en plutôt : « Un train quitte Grenoble à 6h. Il roule à 72km/h. Un autre train quitte Annecy à 8h. Il roule à 69 km/h. À quelle heure et à quelle distance de Grenoble vont-ils se rencontrer ? Grenoble et Annecy sont distantes de 87 kilomètres ».
À vos calculettes ou cahiers de brouillon pour trouver maintenant les résultats de tous ces exercices.
Jean-Louis Hebrard